PROJECT OVERVIEW
This project explored the numerical modeling of incompressible 2D laminar flow in a channel using the vorticity–stream function formulation—a robust method to simplify and solve the Navier-Stokes equations without directly involving pressure.
The primary objective was to:
- Accurately simulate velocity and streamline profiles within a 2D channel of aspect ratio 5:1.
- Validate the outlet velocity profile against the theoretical fully developed laminar flow solution.
METHODS & APPROACH
Governing Equations
Reformulated Navier-Stokes equations in terms of vorticity (ω) and stream function (ψ), eliminating the pressure variable.
Discretization Techniques:
- Central Difference Method for spatial derivatives (second-order accuracy).
- Jacobi Iteration for solving the Poisson equation related to ψ.
- Upwind Scheme for stabilizing convective terms in the vorticity transport equation.
Boundary and Initial Conditions:
No-slip at top/bottom walls, prescribed velocity at inlet, and gradient continuity at outlet.
Stability Constraint
Enforced Peclet number < 0.25 for stable explicit time advancement.
Simulation Setup
2D channel: 61×41 grid points, Δt = 0.001 s, Re = 250, inlet velocity = 1.0 unit.
Implemented in MATLAB 2024 for numerical solution and visualization.
RESULTS & ANALYSIS
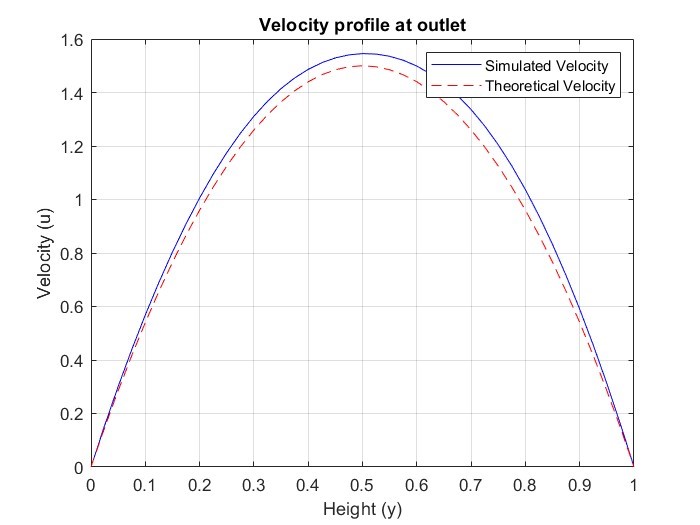
VELOCITY PROFILE
- The simulation output matched the analytical solution for parabolic laminar flow.
- Maximum velocity occurred at the channel centerline, confirming correct implementation.
- Boundary velocities converged to zero, validating the no-slip condition.
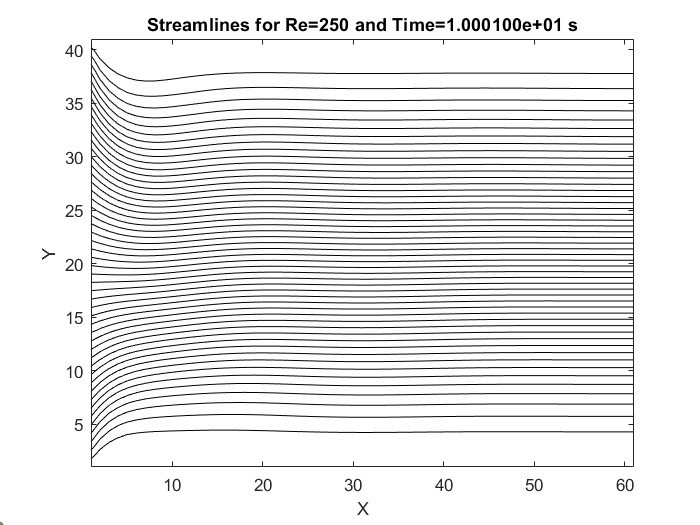
STREAMLINE VISUALIZATION
- Developed flow showed parallel streamlines at the outlet.
- Initial perturbations near the inlet were present but diminished downstream, indicating development toward steady laminar flow.
TOOLS & TECHNOLOGY
- Software: MATLAB 2024
- Methods Used: Finite difference method, iterative solvers, vorticity–stream function formulation
- Mathematical Models: Modified Navier-Stokes equations for incompressible 2D flow
IMPACT
Demonstrated how classical fluid dynamics problems can be solved efficiently using scalar formulations
Reinforced the importance of numerical stability, convergence criteria, and boundary treatment in CFD.
Provided a solid base for extending simulations to more complex geometries, unsteady flows, or thermal coupling in future work
FUTURE WORK
- Introduce finer grid refinement to capture early flow development more accurately.
- Expand to transient or 3D laminar/turbulent cases.
- Integrate heat transfer for conjugate flow modeling in thermal-fluid systems.