PROJECT OVERVIEW
The Problem
Accurately predicting material stiffness is vital in mechanical engineering but traditionally relies on costly and time-intensive simulations or experiments.
The Goal
To develop a machine learning model capable of predicting material stiffness based on microstructural features, offering a faster, cost-effective alternative to conventional methods.
The Context
With access to a dataset of 6,230 training and 2,670 test samples containing 15 features each, this project leveraged machine learning to model complex, nonlinear relationships inherent in material behavior.
METHODS & APPROACH
Your Contributions
With access to a dataset of 6,230 training and 2,670 test samples containing 15 features each, this project leveraged machine learning to model complex, nonlinear relationships inherent in material behavior.
Your Methodology
- Applied brute-force feature selection to remove low-impact inputs.
- Standardized data using StandardScaler.
- Built a neural network with 64 hidden units and Leaky ReLU activation.
- Used the Adam optimizer and MSE loss function.
- Conducted batch training (epochs: 200) on GPU-enabled devices when available.
Your Unique Angle
Integrated empirical tuning of batch size, feature size, learning rate, and activation slope to achieve optimal performance, moving beyond baseline linear models.
OUTCOME & IMPACT
Results
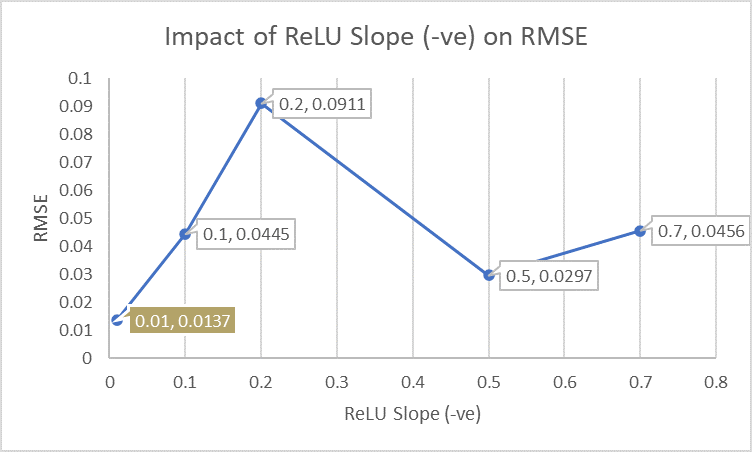
Neural Network RMSE: 0.0137
Key Insights
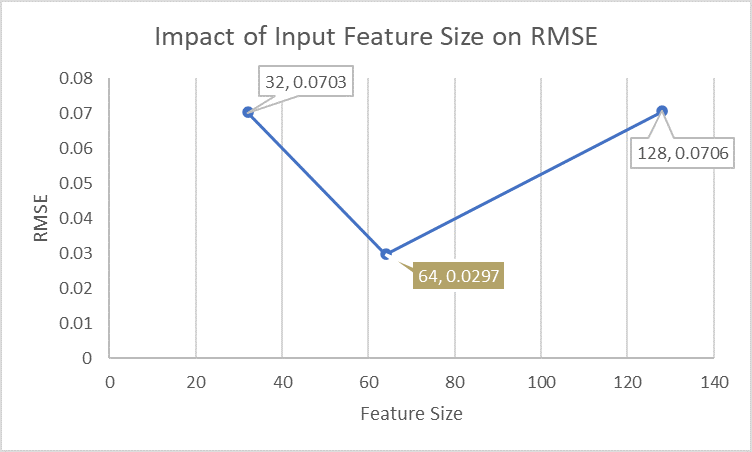
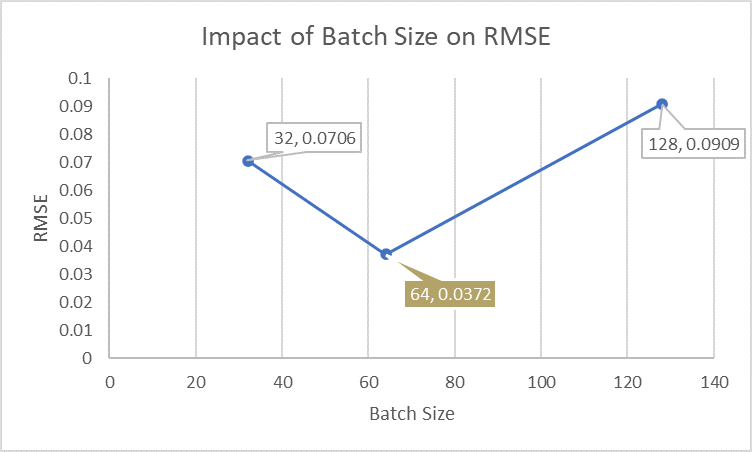
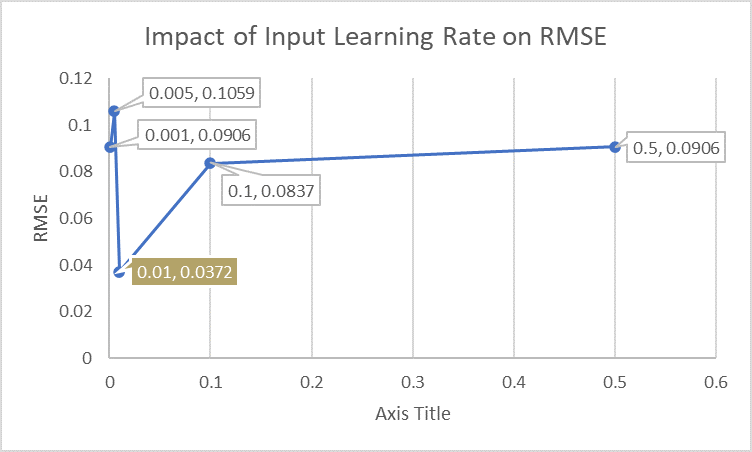
Best results achieved with batch size = 64, feature size = 64, learning rate = 0.01, and Leaky ReLU slope = 0.01.
Visualizations confirmed strong prediction alignment and model convergence.
Business/Academic Impact
The approach demonstrates the power of ML in reducing time-to-insight for material analysis, with potential applications in digital twin systems, smart manufacturing, and accelerated R&D.
LESSONS LEARNED & FUTURE PLANS
What You Learned
Developed end-to-end experience with neural networks for regression, including model design, training loop implementation, performance evaluation, and hyperparameter tuning.
Future Applications
The framework can be extended to other mechanical properties or integrated into physics-informed neural networks (PINNs) for more constrained and accurate models.
Next Steps
- Perform automated hyperparameter tuning (e.g., grid or Bayesian search).
- Expand dataset and refine feature selection techniques.
- Integrate domain knowledge to improve model interpretability and robustness.